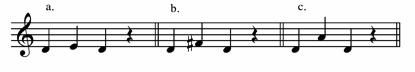Article By David Banney
If one sings a major second, a major third or a perfect fifth, one has the strong impression that the bottom note is ‘home’, or do. Try singing the examples in Fig 1 – in each case there is little ambiguity, the only exception being Fig 1a (Way up high), in which so-la may be comfortably substituted for do-re, though there is still no doubt that it is the bottom note and not the top note that feels like home.
Figure 1 – Major second, major third, perfect fifth. In each case the lower note feels like ‘home’.
This feeling breaks down when we sing a perfect fourth. In a perfect fourth it is the top note that feels like home. If a perfect fourth is played as a chord, it has an empty, incomplete (dissonant) quality that may be remedied by doubling the top note one octave lower. In Fig 2, the first chord sounds dissonant, while the second chord sounds consonant. Note that the second chord has a perfect fifth at the bass.
Figure 2 – A perfect fourth sounds ‘incomplete’ or dissonant.
Why should this be so? The answer requires an understanding of two important acoustical phenomona – the harmonic series, and the notion of the beat frequency.
The Harmonic Series
The harmonic series is a collection of inaudible sounds produced whenever a note is played. The frequencies of the notes in the series are predictable – they are all of the multiples of the frequency of the fundamental note (i.e the note being played). Thus, for the note A in Fig 2, which has a frequency of 110 cycles per second (110Hz), the notes of the harmonic series are 110 x 2, 110 x 3, 110 x 4, 110 x 5 etc. The series continues to infinity, though usually the fundamental frequency is the only one that can be heard.
The harmonic series is shown on the staff in Fig 3, where it can be seen that the first six notes – A, E and C# – make up an A major triad. It can also be seen that there is a perfect fourth between the 3rd and 4th notes, E and A.
Figure 3 – The harmonic series, built on A = 110Hz
The Beat Frequency
The beat frequency is best understood by imagining two people playing an A slightly out of tune with each other – one playing A=440, and the other playing A=441. The result, apart from the pair of out of tune notes, is a wobble in the air known as the ‘beat’. The frequency of the beat can be calculated as the difference in frequency of the two notes. In this case, 441-440 = 1, therefore the beat frequency is one cycle per second (1Hz). If the first note is changed to 442Hz, the beat frequency would become 2Hz (442-440 = 2Hz). If the first note is changed to 440Hz, the beat frequency would be 0Hz (440-440 = 0)., and the two notes would sound ‘in tune’.
While string players are generally well acquainted with the idea of the beat frequency as a product of two out of tune notes (we exploit this phenomenon when we tune our strings), it is often overlooked that in fact any pair of different pitches, in tune or not, produces a beat frequency. Returning to the harmonic series, if the first two notes are played together (220Hz and 110 Hz) the beat frequency will be 110Hz (220-110 = 110). Thus, the beat frequency of an octave is the same as the lower note of the octave, and it is for this reason that octaves sound so resonant (Fig 4a).
Figure 4 – Beat frequencies of successive notes of the harmonic series. In each case the beat frequency is the bottom note (or fundamental) of the series.
If the next two notes of the series are played together (330 Hz and 220Hz), the beat frequency is, again, 110Hz (Fig 4b). Thus, the beat frequency of a perfect fifth is the note one octave below the bottom note of the fifth. The bottom note of the fifth is reinforced, and we hear strongly that the bottom note is ‘home’.
Coming to the next two notes of the series (440 Hz and 330Hz), yet again the beat frequency is the note at the bottom of the series (110Hz) (Fig 4c). Thus the beat frequency of a perfect fourth reinforces not its bottom note (E) but its top note (A). Naturally, the listener does not consciously hear this beat frequency (although beat frequencies of fourths and fifths and thirds can sometimes be heard especially when high notes are used), but one senses a deeper note, and it is this phantom note that reinforces the top note rather than the bottom note of a perfect fourth.
Implications for Tonality and sol-fa
It can now be understood that when a perfect fourth is heard (without any prior harmonic context), we sense the top note as home. In sol-fa, we would sing the fourth as so-do’ rather than do-fa.
This has implications for melodies that have a span of a perfect fourth. Excluding tetratonal melodies that use mi-so-la (eg Fig 5a), other such melodies span either so-do’ or do-fa. A tetratonal example may be seen in Fig 5b, while tetrachordal examples are shown in Fig 5c – f.
Figure 5 – Examples of tetratonal and tetrachordal melodies
In each case in Fig 5 the sol-fa of the first note is given. In the tetratonic melody in Fig 5b, the perfect 4th is felt as so-do’. This seems to be the case for all melodies using this pitch class set.
In Fig 5c, the melody opens with a trichordal phrase, clearly setting up the bottom note as do. The appearance of the 4th in measure 3 does not alter the sense of tonality, so in this case the perfect 4th is heard as do-fa. In Fig 5 d, the strong reiteration of the E on the downbeat seems to direct the ear towards C rather than F as do. Thus, the perfect fourth in this tetrachord is, again, do-fa.
In Fig 5e and f, the opening interval is a fourth. In each case the upper note is clearly felt as do’, and the perfect 4th as so-do’.
Finally, several examples from art music illustrate the point (Fig 6).
Figure 6 – Tetrachordal examples from art music
In each example the end of a tetrachordal phrase or fragment is shown with an asterisk. In the first example (Fig 6a) the end of the first phrase feels incomplete, and is harmonically completed by the next phrase. The perfect 4th in the first phrase is so-do’. The second example (Fig 6b) establishes the bottom note as home (although it is perhaps more ambiguous than other examples shown), and this is confirmed by the next phrase. Here the perfect 4th of the first phrase is do-fa.
Fig 6c shows an unambiguous so-do’ tetrachord. Fig 6d, like 6b, is somewhat ambiguous, but the answering phrase confirms C as do, and thus the perfect 4th opening tetrachord is do-fa.
What are the ‘Rules’?
There are no ‘rules’ for deciding whether a tetrachordal phrase or melody is do-fa or so-do. However, the following guidelines may be helpful:
- If the tetrachordal phrase/melody begins by emphasizing the perfect 4th, it is likely to be so-do’;
- If the beginning emphasizes the lower three notes of the tetrachord, it is likely to be do-fa;
- If there is an anacrusis, consider the strong possibility that the downbeat is do.